
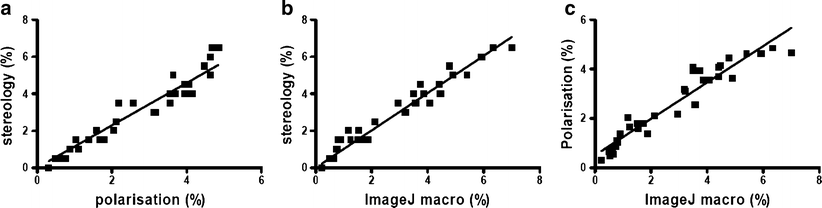
Find the parameters such as Bone Volume, Trabecular thickness and trabecular number in a given sample of bone.calculating the total length of capillaries per unit volume of a biological tissue, by counting the number of profiles of capillaries per unit area on a typical histological section of the tissue (multiplied by 2).calculating the surface area of pores per unit volume in a ceramic, by measuring the length of profiles of pore boundary per unit area on a typical plane section of the ceramic (multiplied by 4 / π ).calculating the volume fraction of quartz in a rock by measuring the area fraction of quartz on a typical polished plane section of rock ("Delesse principle").It is a completely different approach from computed tomography.Ĭlassical applications of stereology include: Cavalieri's principle) and statistics (mainly survey sampling inference). Stereology is based on fundamental principles of geometry (e.g. Hence, stereology is often defined as the science of estimating higher- dimensional information from lower-dimensional samples. It is especially useful when the sample has a lower spatial dimension than the original material. needle biopsy), projected images, and other kinds of 'sampling'. 3D microscope images), one-dimensional probes (e.g. In addition to two-dimensional plane sections, stereology also applies to three-dimensional slabs (e.g. New innovations such as the proportionator continue to make important improvements in the efficiency of stereological procedures. Stereology is a developing science with many important innovations being developed mainly in Europe. It is an important and efficient tool in many applications of microscopy (such as petrography, materials science, and biosciences including histology, bone and neuroanatomy). Stereology is a method that utilizes random, systematic sampling to provide unbiased and quantitative data. It provides practical techniques for extracting quantitative information about a three-dimensional material from measurements made on two-dimensional planar sections of the material. Stereology is the three-dimensional interpretation of two-dimensional cross sections of materials or tissues. JSTOR ( July 2020) ( Learn how and when to remove this template message).
Unsourced material may be challenged and removed. Please help improve this article by adding citations to reliable sources.
This article needs additional citations for verification.


 0 kommentar(er)
0 kommentar(er)
